Eukleidovská konstrukce

Postup narýsování pravidelného šestiúhelníku Eukleidovskou konstrukcí

Eukleidovská konstrukce neboli konstrukce pomocí kružítka a pravítka označuje konstrukci geometrických objektů (například úhlů) pouze pomocí idealizovaného pravítka a kružítka. O pravítku se předpokládá, že má nekonečnou délku, jen jednu hranu a žádné značky pro měření, o kružítku se předpokládá, že může nakreslit jakkoli velikou kružnici.

Tento pojem se vyskytuje především v zadání matematických úloh. Úkolem bývá určit, zda z daného objektu je možné pomocí Eukleidovské konstrukce vytvořit jiný objekt, který má dané vlastnosti. Příkladem jsou klasické řecké úlohy trisekce úhlu, kvadratura kruhu a duplikace krychle. Lze dokázat, že ani jednu z těchto úloh pomocí Eukleidovské konstrukce vyřešit nelze.

Základní konstrukce

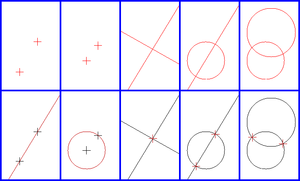
Každá Eukleidovská konstrukce se skládá z opakování pěti základních konstrukcí s pomocí bodů, úseček a kružnic, které byly vytvořeny již v předchozích krocích. Celkový počet kroků musí být konečný. Mezi základní konstrukce patří

Vytvoření úsečky protínající dva body

Vytvoření kružnice se středem v jednom bodě tak, aby protínala druhý bod

Vytvoření bodu, který leží v průsečíku dvou protínajících se úseček

Vytvoření jednoho nebo dvou bodů ležících v průsečíku kružnice a úsečky (pokud se protínají).

Vytvoření jednoho nebo dvou bodů ležících v průsečíku dvou kružnic (pokud se protínají)

Například rovnostranný trojúhelník lze vytvořit ze dvou různých bodů A a B následujícím postupem.

Vytvoříme úsečku protínající body A a B
Vytvoříme dvě kružnice, jednu se středem v bodě A protínající B, druhou se středem v bodě B protínající A.
Vytvoříme dva body (C a D) v průsečíku obou kružnic
Vytvoříme dvě úsečky, jednu protínající A a C, druhou protínající B a C

Výsledkem je rovnostranný trojúhelník s vrcholy A, B a C.

Konstruovatelná čísla

Eukleidovskou konstrukcí lze následovně vytvořit osy souřadnic: Mějme dva body A a B. Vytvořením přímky protínající A a B získáme osu x s nulou v bodě A a jednotkou v bodě B. Spuštěním kolmice (ta je také konstruovatelná) v bodě A vytvoříme osu y. Vytvoříme kružnici se středem v A protínající B a v průsečíku s osou y získáme jednotku i na druhé ose.

Bodům (x,y) v tomto Eukleidovském prostoru lze přiřadit komplexní čísla x + y i. Bod (x,y) je konstruovatelný, pokud ho lze Eukleidovskou konstrukcí vytvořit pouze z počátečních bodů A a B. Lze ukázat, že takto lze zkonstruovat všechny body x + y i pro racionální x a y. Zároveň lze pro každá konstruovatelná a a b zkonstruovat a + b, a – b, a × b a a / b. Konstruovatelná čísla tedy tvoří těleso, které je podtělesem komplexních čísel. Navíc platí, že pro každé konstruovatelné a lze zkonstruovat i ${\sqrt {a}}$ . Všechna konstruovatelná čísla jsou algebraická, proto není konstruovatelné žádné transcendentní číslo jako např. $\pi$ a proto není možná kvadratura kruhu.

Konstruovatelné úhly

Lze dokázat, že existuje bijekce mezi konstruovatelnými úhly a body konstruovatelnými na konstruovatelných kružnicích. Konstruovatelné úhly tvoří komutativní grupu se sčítáním modulo 2π. Úhel je konstruovatelný právě když číslo odpovídající jeho tangensu (nebo ekvivalentně i sinu a kosinu) je konstruovatelné. Například pravidelný sedmnáctiúhelník je konstruovatelný, protože

$\cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}$

jak dokázal Carl Friedrich Gauss.

Konstruovatelné pravidelné mnohoúhelníky

Nakreslení pravidelného pětiúhelníku Eukleidovskou konstrukcí

Některé pravidelné mnohoúhelníky lze Eukleidovskou konstrukcí vytvořit jednoduše, jiné ne. To vedlo k otázce, zda lze takto vytvořit všechny mnohoúhelníky. Carl Friedrich Gauss v roce 1796 ukázal, že pravidelný n-úhelník lze Eukleidovskou konstrukcí vytvořit, pokud liché dělitele n jsou různá Fermatova prvočísla. Gauss se správně domníval, že tato podmínka je nejen nutná, ale i postačující, ale dokázat se to podařilo až Pierru Wantzelovi v roce 1837.

Konstrukce pěti a desetiúhelníku: 1.úsečka A,B se středem S. 2.kružnice k o poloměru AS. 3.Na AS bod O tak, že AO=OS 4.bodem S kolmici na AB, v průsečíku k s kolmicí pak body C a D 5.z O kružnicí o poloměru OC protnout SB a průsečík označit E. 6.úsečka CE je strana pětiúhelníku a SE desetiúhelníku.

Literatura

HEATH, Thomas. The Thirteen Books of Euclid's Elements. New York: Dover Publications, 1956. Dostupné online.
SERVÍT, František. Eukleidovy základy. Praha: 1906. Dostupné online. (česky)
ŠÍR, Zbyněk. Řecké matematické texty. Praha : Oikoymenh, 2011. 570 s. ISBN 978-80-7298-308-7. (česky)
GÁL, KAMARÝT. Opakování středoškolské matematiky

Související články

Externí odkazy

Obrázky, zvuky či videa k tématu eukleidovská konstrukce na Wikimedia Commons
Anglické zpracování Eukleidových Základů na internetu

Pahýl

Tento článek je příliš stručný nebo postrádá důležité informace.
Pomozte Wikipedii tím, že jej vhodně rozšíříte. Nevkládejte však bez oprávnění cizí texty.